Probability Theory in Machine Learning: An example with exponential distributions

Probability theory was born for games of chance in the 16th century

Every day we have to deal with the uncertainty & randomness that life-events present us. To take rational decisions and have better expectation of their future outcomes, we have probability theory.

Although, there is a decrease of the level of math needed for machine learning engineers (due to the increase of empirical data exploitation), having a good command of linear algebra, probability theory & calculus is a necessity for shaping an intuition why the models work the way they do or why they fail.

Let me give you a simple example of how probability distributions played a central role in a machine learning classification problem.

The discussed terms (briefly) are the following:

Roadmap:

Part 0: My bayesian-classification example

With this machine learning problem in mind, I gathered all the really pre-basic concepts in a page divided in four parts (you can find it below).

1. Product distribution
2. Optimal Stopping Problem
3. Exponential Family
4. Conjugate Prior

Part 1: Physical Probabilities

Experiment or Hypothesis || Sample Space & Random Variable || Event

Part 2: Probability Distribution Function

Probability distribution table|| Probability Mass Function || Probability Density Function || Behavior of a Distribution

Part 3: Evidential Probabilities

Bayesian Probability || Bayesian & Frequentist Interpretation of Probability

Part 4: Fundamental Rules of Probability

Sum || Product

Next Post: Computing Probability Distributions in Python

Although, Bayesian statistics are the commonly used in machine learning, I thought it’s worthy comparing them with the frequentist interpretation of probabilities.

Bayesian Setting

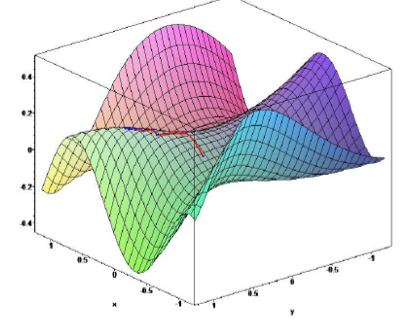
We have two independent random variables’ distributions, Bernoulli (with parameter θ[0, 1]) & Exponential (with parameter λ), as inputs in simulation experiments. The former represents a sequence of independent, identically distributed of action’s correctness; and the latter reflects the speed until the action is completed.

The product distribution of these two defines a third variable that reflects one’s mastery of a goal (set of actions) and also has the interval [0,1] as domain. This is going to be fed in an optimal stopping problem where the output is modeled similar to that of coin tossing, as described below.

The optimal stopping problem: you wish to maximise the amount you get paid by choosing a stopping rule (optimization). You have a set of i.i.d actions that you repeatedly solve. Each time, before you have received a new action, based on the stopping rule, you can choose either to stop, get paid (let’s say in correct actions’ points), and progress to the second goal or to continue practicing with the the first goal (Binary classification).

The free parameters, θ and λ, which shape the behaviors of these two distributions (and hence also the third), are unknown. We know that both distributions belong to the Exponential Family, which gives us the ability to utilize their property of Conjugates priors. The latter offer a closed-form solution (can be evaluated in a finite number of operations) to our posterior. In a bayesian setting, we learn/estimate the parameters as incoming data updates their values via a simple update rule instead of gradients computation.

If the posterior distributions p(θ | x) are in the same probability distribution family as the prior probability distribution p(θ), the prior and posterior are then called conjugate distributions

The priors of Bernoulli and Exponential will be estimated by drawing them from their conjugates, Beta and Gamma, respectively:

f(x): Posterior (Beta)= Likelihood Bern(n, θ) * Prior on θ Beta (a,b), a-1 correct actions, b-1 incorrect

f(y):Posterior (Gamma) = Likelihood Exp(λ) * Prior on λ Gamma(n,λ), n-1 observations that sum to λ

Exponential family distributions:
1. Gaussian,
2. Exponential,
3. Beta,
4. Gamma,
5. Binomial,
6. Poisson.

My next step is to refresh continuous and discrete probability distributions, which belong to exponential family, together with some of their inherent properties like the memoryless property and conjugate priors. Although, distributions don’t necessarily have an intuitive utility, I’ll try to go through simple examples to gain some intuition. Beside that, I’ll try to understand the following:

• how the distributions model random variables to form a likelihood function,
• a property related to each distribution that makes them “desirable” (i.e. poisson point process, central limit theorem),
• the parameter space,
• & the mass or density functions.

To fill this theoretic-heavy job with fun, I’ll use Python libraries (scipy, pandas, numpy, matplotlib) to

(i) make plots with different behaviors for each of the above distributions &(ii) simulate random variables generated by them.

Next steps:

0. Computing Probability Distributions in Python (coming soon)

1. The best intro: Chapter 1.2, Pattern Recognition and Machine Learning
2. A quick reminder: Probability Cheatsheet

2. In a short video: Mathematics of Machine Learning

3. Detailed Course: MIT

Until then, Hap-py-coding ⇧⏎

Feel free to respond, ask a question, express a request or correct a mistake you may find.